項式と多 の 乗法、除法(2) 単項式と多項式の乗法につい て学ぼう ①多項式と単項式の乗法はどうす ればよいか 長方形の面積を、文字を使って表すこと で、数と多項式の乗法と同じように分配法則 が使えることを見い出す。 多項式と単項式の乗法は、数と 単項式とは 項が つだけの式 のこと、多項式とは 項が つ以上ある式 のことです。項が単数(1つ)の式は「単項式」 項が多数の式は「多項式」 というわけなんだね。 先生がはじめに例であげたx 2 +5xy-6は、 x 2 、+5xy、-6と項が3つあるから多項式というわけなんだ。

高校数学 多項式の次数 練習編 映像授業のtry It トライイット
多項式のこう
多項式のこう-基本用語 1変数の多項式 不定元 x に関する(1変数の)多項式とは、 という形の式のことをいう。これを = とも書く。ただし、 n は非負整数で、 a n, a n − 1, , a 0 は数である。 各々の a k x k (k = 0, , n) のことを項(より詳しくは k 次の項)とよび、 a k をその項の係数とよぶ。2 多項式の乗法 多項式と多項式との乗法は,分 配法則をもとにして行われるこ とを知り,展開することができ る。 展開する 多項式と多項式との乗法に関心 をもち,その計算を行おうとし ている。 多項式と多項式との乗法に関心



Www City Tatebayashi Gunma Jp School Chu Daini Corona nensuugakukadai Pdf
ニュートン多項式の基本対称式での表示式を求め、項の係数の法則性を調べる。 方針 いきなり の表示式を求めるのは難しいので、以下の順を追って調べていく。 の表示式を調べる。 の表示式を調べる。数学 、 初等代数学 における 多項式 の 次数 (じすう、 英 degree )は、多項式を 不定元の冪積 の 線型結合 からなる 標準形 ( 英語版 ) に表すとき、そこに現れる項のうち最も高い項の次数を言う。多項式と単項式は 「項が一つ以上か、一つか」 の違いだけ! 多項式の次数の定義は、「最も高い項の次数」なので、そこには注意しよう。 多項式×多項式の計算も、単項式×多項式のときに 分配法則が成り立つ ことを用いれば計算できる!
つまり、項が二つ以上あり、単項式の形に出来ないものが多項式といえます! 次数とは? 単項式と多項式がどのようなものなのかを説明しましたが、これらをさらに分類することができます。 何で分類するのかというと、掛けられている文字の数です! 問題 次の多項式を、\(a\) について降べきの順に整理し何次式になるか答えよ。 また、定数項を求めよ。$${\small (1)}~52a^25a3a^27a3$$$${\small (2)}~3ab2.も1と同様で、`c_n` の一般項から、この一般項が 0 を取り得ないことをいうか、 あるいはチェビシェフ多項式 `T_n(x)` の根はどんな `n` に対しても `x = 06` とはなりえないことをいう。
多項式 2ab , 3x−4y のように単項式の和の形で表される式を多項式といいます。( 3x−4y は 3x(−4y) と書くことができ、 −4y の係数は −4 です。) 多項式を構成しているそれぞれの単項式を項Collect は多項式の項をまとめることができる. 多項式を定義して x の累乗をまとめる: Collect 内で項を簡約することもできる:項式に相当する多項式はKoornwinder多項式と言います 普通, Gaussの超幾何函 数が多項式に退化する場合ってJacobi 多項式ですよね で, Jacobi 多項式ってい うのは次数nと ;



必修 4 10 多項式の項の個数と二項定理 わかりmath



Http Shiraito Maizuru Ed Jp Library Zmath2 1 1 Pdf
符号のブール多項式表現 n ブール体 GF(2) n 符号長nの符号語 に対して,ブール体GF(2)の要素{0, 1} を係数とするブール多項式 ) をvの多項式表現と呼ぶ.V(x)は符号多項式と呼ばれる. v = (v n1,L,v 1,v 0) v i ˛{0,1} 0 1 1 1 V(1 x vI Rの上の多項式とは,すべての項の係数がR の要素である多項式 I つまり,ある自然数n 0と実数a0;a1;;an に対して a0 a1xa2x2 anxn と,変数xを用いて書ける式のこと 注意:上の多項式を ∑n i=0 aix i と書くこともある 多項式の次数とは?情報符号理論 16 11 通信路符号化法 ― 巡回符号 西田豊明 2 / 13 à0,1を係数とする 次の多項式の周期は高々2 −1である.なぜならば, á−1という多項式 を 次多項式 à à⋯ 1 0で割り算をする状況を考えると,出現する剰余は, à−1




多項式




単項式と多項式はこれでok 今を懸命に生きるオーちゃん
教科書P10,11 1.単項式と多項式 課題(P10 ) 1 次の式を,項が1つの式と,項が2つ以上ある式に分けよう。 4 a x2-9 2 x2-3x-2 -3 xy7 2 ab-y -2 ・項が1つだけの式 項が1つだけの式を( )と いう。 とみることができる。多項定理は教科書には登場しませんが, k = 3 k=3 k = 3 の場合については軽く言及されています。 数学2の教科書に載っている公式の解説一覧 この記事の編集者 マスオ 高校数学の美しい物語の管理人。 「わかりやすいこと」と「ごまかさないことこんにちは、あすなろスタッフのカワイです。 多項式同士の掛け算には、4つの公式があります! 今回は、この公式はどのように導き出されたものなのか、そして実際の計算でどのように用いられるかについて解説していきます! 関連記事




1研究中 C 数学5 単項式 多項式 整式 分数式 有理式 無理式 係数 項の次数次式元



1
性質 編集 全ての最小多項式は既約であるから,原始多項式は既約である. 原始多項式の定数項の係数は非零でなければならない.そうでないと,多項式 x で割り切れてしまう.GF(2)においては, x 1 は原始多項式であるが,それ以外の全ての原始多項式は奇数個の項を持つ.なぜなら「多項式(たこうしき)」は、2つ以上の「項」を足し算している式 のことなんだ。 ちなみに、 一つの項だけからできている式を「単項式(たんこうしき)」 というんだ。 「多項式」を何に使うかって多項式の計算① 1章 式の計算 教科書 P12~14 1 5xy, 1 2 a2 などのように,数や文字についての乗法だけでつくられた式を単 たん 項 こう 式 しき という。a や-2 のような1 つの文字や1 つの数も単項式と考える。 -7ab+2c のように,単項式の和の形で表された式を多 た




整式 単項式 多項式 の計算 勉強動画ラボ 高校数学を中心とした無料の学習動画まとめ




中学2年生 数学 式の計算 多項式の計算 問題プリント 無料ダウンロード 印刷 このページの問題プリント 全部
Point:同類項 多項式を整理するとき、まずは同類項(=次数が同じ項)をまとめましょう。 また、降べきの順とは整理された多項式で次数の高いものから順に並べることをいいます。 例えば$$~~~~~x^23x25x^24x3$$$$~=x^25x^23x4x23$$$$~=6x^2x1$$多項式の次数 単項式の和の形で表された式を 多項式 といいます。 $$2ab, x^23x4, 2xy^34x$$ このように項が複数ある式が多項式ですね。 多項式の次数を考える場合には任意の二項型多項式列はシェファー列だが、逆は必ずしも成り立たない。多項式列は19世紀の漠然とした umbral calculus の概念を下敷きにしている。 二項型多項式列の概念は組合せ論、確率論、統計学、その他さまざまな分野に応用を持つ。




中学2年数学 式の計算 単項式と多項式とは その次数と係数もマスターしよう 数学の面白いこと 役に立つことをまとめたサイト



Http Www Sakasai J Kashiwa Ed Jp Action Common Download Main Upload Id 2163
光学用語集 ゼルニケ近似多項式(Zernike polynomial) 光学系の波面収差は光線が瞳を通過する座標をx,y として W( x, y ) として表されます。 実際は各 x, y に対して対応する波面収差 Wi( x, y ) ( i = 1, 2, ,n ) が光線追跡により求まります。続いては多項式の減法ですが、こちらは加法と異なり 符号に注意が必要 です。 多項式の減法では、 ひく方の式の各項の符号を変えて 、すべての項を加えます。 (2) $(2xy)(x3y)$ かっこをはずす $=2xy\textcolor{blue}{}x\textcolor{blue}{}3y$ 同類項をまとめる $=\textcolor{blue}{x4y}$多項式曲面近似における多項式の項の定義 x および y 入力の次数を指定することにより、多項式曲面モデルに含まれる項を制御できます。i が x の次数で j が y の次数の場合、多項式全体の次数は i および j がその上限です。




Opi Times3 18 18 Lihat Cara Penyelesaian Di Qanda




3分で分かる 多項式とは 加法 減法 乗法についてわかりやすく 合格サプリ
次数について(多項式の場合) 多項式の次数は, 各項のうちもっとも次数の大きいもの! (例)6 25 項は 6 2と5 6 2 5 の次数は5× だから1 6 25 の次数は 2 こっちのほうが大きい!この多項式を\(x\)についての降べきの順に並べるとこのようになります。 \(2x^{3}3x^{2}5x4\) 多項式の項を\(x\)の次数が下がっていく順に並び替えました。 この作業のことを降べきの順に並び替えるといいます。 単項式と多項式の違い正則化項を導入した際の回帰係数 正則化項を導入すると係数の値が小さく抑えられる lassoにはいくつかの係数が0となる スパース(疎)な解が得られやすいという特徴がある 正則化項を導入した9次多項式回帰の係数 lassoでは スパースな解が 得られる



Www City Tatebayashi Gunma Jp School Chu Daini Corona nensuugakukadai Pdf




同類項と多項式の計算 基礎 教遊者
今回のテーマは「単項式と多項式」だよ。 みんなは中1数学で学習した「項」という言葉は覚えてるかな? 項 とは、 +や-の符号で区切ったときの1つ1つの数のこと をいったね。 では「単項式」と「多項式」がそれぞれ何を表すのかわかるかな?




数と式 多項式の次数 何次式って何 多項式の次数の数え方の巻 Vol 4 3回読めば 絶対理解できる看護受験数学 Kazアカデミー 大阪の看護学校 看護予備校




3分でわかる 多項式の解説 次数 昇べき 降べきの順をわかりやすく 合格サプリ




本時の目標 用語の意味を理解する 同類項をまとめて2つの文字をふくむ式の加法 減法をすることができる Ppt Download




円分多項式 Wikipedia




単項式 項 多項式 整式 定数項の違いを教えてほしいです Clear



多項式の次数説明のしかた 中学2年数学 数学が苦手な中学生に理解しやすいよ Yahoo 知恵袋




文字式 5 項と係数 伊東市の家庭教師




高校数学 多項式の次数 練習編 映像授業のtry It トライイット




多項式について 中学数学であいまいな点をはっきりさせよう 身勝手な主張



多項式の係数は 1分でわかる求め方 例題 次数との関係




中学数学2年 単項式と多項式とその次数 受験の月




1 3a2 2 5ab 3 Dfr Lihat Cara Penyelesaian Di Qanda



1




多項式について 中学数学であいまいな点をはっきりさせよう 身勝手な主張




高校の課題です Clear



q 次の多項式の同類項をまとめ 次数の大きい項から順に並べて書きなさい Yahoo 知恵袋




単項式 多項式と次数 ときどき係数 教遊者




中2 単項式と多項式 やませのブログ




文字式 代数式 のルールと単項式 多項式の足し算と引き算 リョースケ大学




3分で分かる 多項式とは 加法 減法 乗法についてわかりやすく 合格サプリ
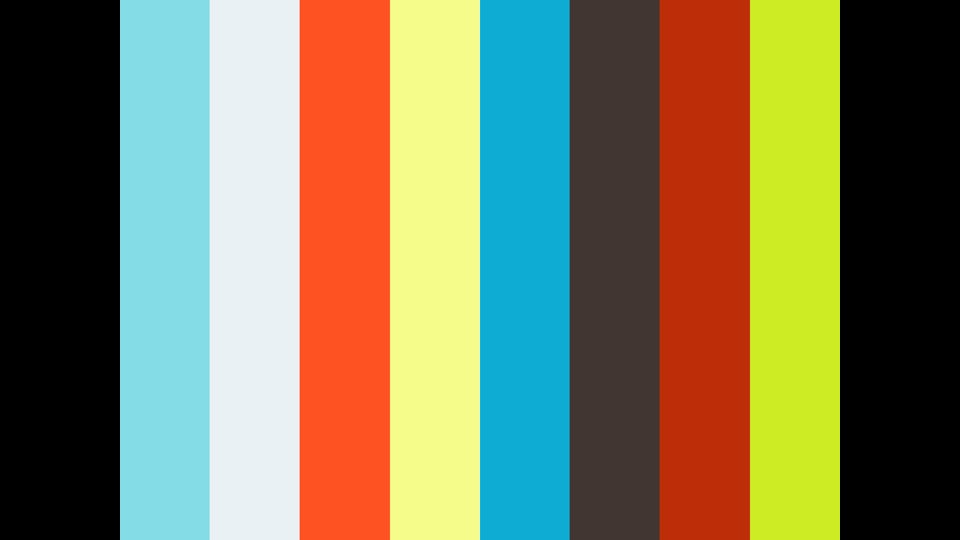



1章1節03 多項式の項とは 中村 翔
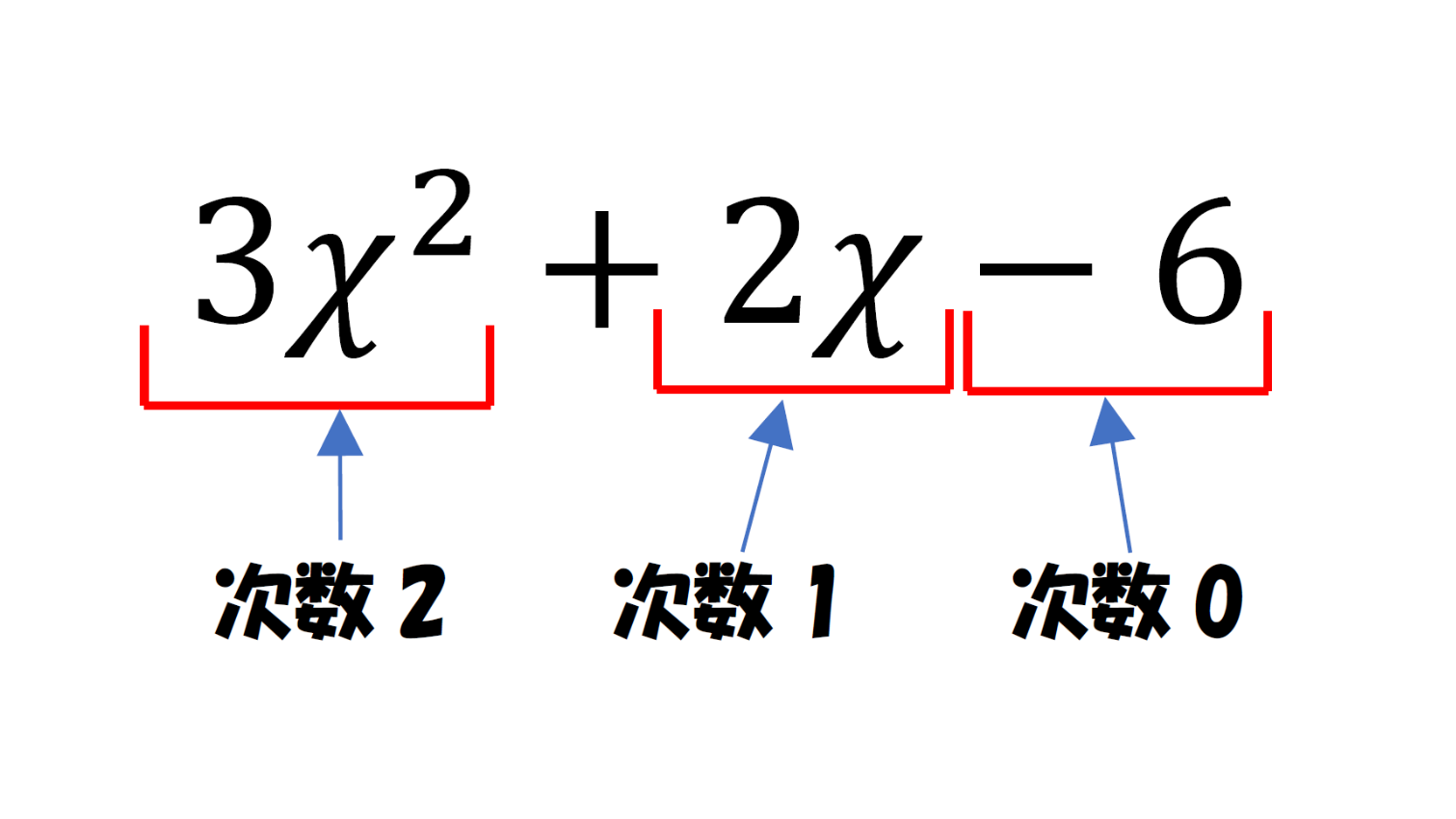



多項式って何 すうがくのいえ




1学期に習う中2数学その1 単項式 多項式 次数 次式 中2 中3 数学 家庭教師とっしゅ先生の授業 小学生 中学生




高校数学 単項式 多項式とは 例題編 映像授業のtry It トライイット
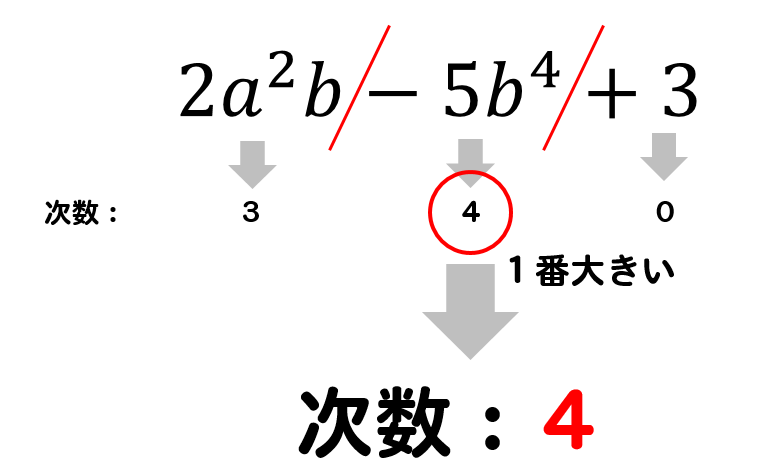



単項式 多項式 何次式 係数 次数の見分け方を解説 数スタ



1
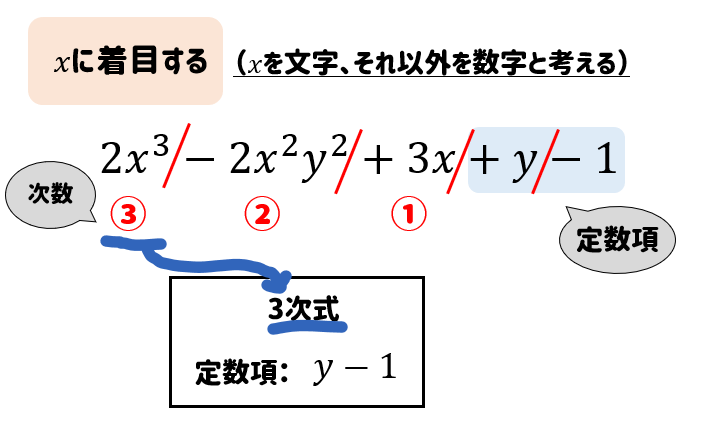



高校数学 文字に着目したときの次数 係数の求め方は 数スタ




差積という多変数多項式の次数を考え対称群へと タロウ岩井の数学と英語 Note




多項式の項と係数のやり方が分かりません 誰か教えて下さい Clear




黒木玄 Gen Kuroki 整式 たとえば09年発行の東京書籍 新編新しい数学2 では 単項式 多項式 という用語を添付画像のように説明しています 1 単項式 は 多項式 ではなく 多項式 は 単項式 ではないというスタイルに見える 続く




高校数学 多項式の次数 練習編 映像授業のtry It トライイット



多項式と単項式とは 項 次数 係数などの意味や計算問題 受験辞典




N倍角の公式を表す多項式 チェビシェフの多項式 の係数の秘密 Yoshidanobuo S Diaryー高校数学の 思考 判断 表現力 を磨こう ー




高校一年の数学 数学 式の計算 整式 整式の加法 減法 展開 因数分解 独学習 予習 復習におすすめ Cars634 S Diary



高校入試 英語 数学 学習 式の計算 単項式と多項式




中2数学 次数と係数 練習編 映像授業のtry It トライイット
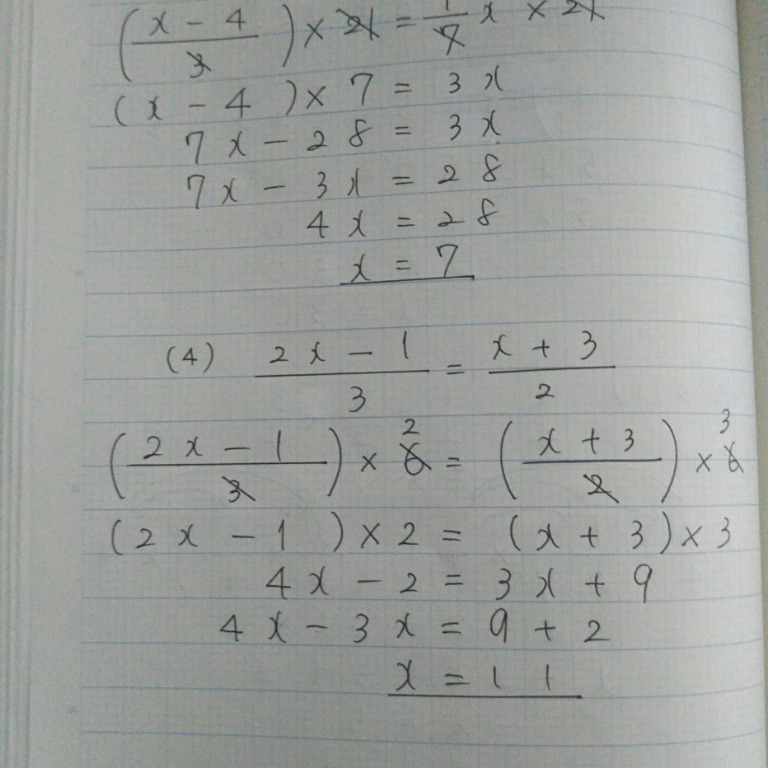



Tossランド 分子が多項式の項をふくんだ方程式




単項式と多項式




単項式 多項式と次数 ときどき係数 教遊者




1 4xy 2 3y2 A 3 Lihat Cara Penyelesaian Di Qanda




多項式の次数の求め方 一番大きい次数を答えるだけだ 中学や高校の数学の計算問題



3




中学数学 何次式 の見分け方をイチから解説 中学数学 理科の学習まとめサイト



中学2年数学 式の計算 同類項とは 同類項をまとめると計算ができる 数学の面白いこと 役に立つことをまとめたサイト




同類項と多項式の計算 基礎 教遊者




高校数学 多項式の次数 例題編 映像授業のtry It トライイット




補足の部分が よくわかりません 教えてください Clear




中学校数学の問題点 単項式と多項式 ベクトル空間や多項式環として眺めれば 身勝手な主張




多項式について 中学数学であいまいな点をはっきりさせよう 身勝手な主張




公式集 1 1 単項式 多項式 定数項などの用語を理解しよう コメディカル受験対策講座




多項式の項の求め方 区切る部分を覚えたらわかる 中学や高校の数学の計算問題




概念2 多項式的項 係數 次數 Youtube




式の計算 単項式と多項式の違いをマスター 次数に注意 中学数学をはじめから分かりやすく




中2 式の計算 単項式と多項式 次数は次の世界を結び付ける 教えたい 人のための 数学講座




中学数学 単項式と多項式 次数と係数 Youtube




多項式の足し算引き算のルールを理解しよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに




式の計算 単項式と多項式の次数の数え方 中学数学 定期テスト対策サイト




単項式と多項式の違い 簡単な問題を解けば違いがわかる 中学や高校の数学の計算問題




数と式 多項式の次数 何次式って何 多項式の次数の数え方の巻 Vol 4 3回読めば 絶対理解できる看護受験数学 Kazアカデミー 大阪の看護学校 看護予備校




単項式と多項式のそれぞれの意味と違い 数と式




中2数学 項と次数 単項式と多項式の次数の求め方と練習問題 Pikuu




中2数学 単項式 多項式 について 式の計算 ひっそりと物理や数学を解説する




単項式と多項式の違いを理解しよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに




多項式の全てがこれでわかる 多項式はこれで完璧だ 高校生向け受験応援メディア 受験のミカタ




多項式と単項式の違いとは 次数や乗除 乗法除法 や分配法則についても解説 遊ぶ数学



2




Kelas 8 Catatan Tentang 単項式と多項式 式の次数 Clear
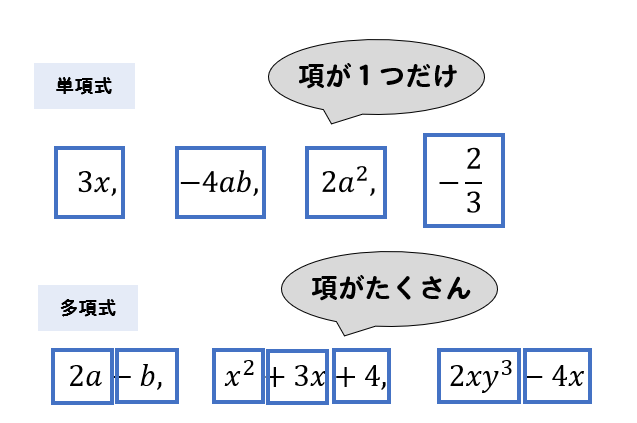



単項式と多項式ってどんな意味 それぞれの違いについて解説 数スタ




問題よ意味と答えが分かりません 教えてください Clear




中学2年生 数学 式の計算 多項式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




単項式




数学 中2 1 単項式と多項式 Youtube




大至急お願いします これの 項はなんですか Clear




式の計算 単項式と多項式の次数の数え方 中学生からの勉強質問 数学 進研ゼミ中学講座
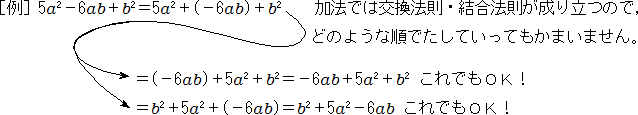



式の計算 多項式を書く順番 中学数学 定期テスト対策サイト




同類項と多項式の計算 基礎 教遊者




中学2年生 数学 式の計算 多項式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




単項式と多項式の違い さわやか さくらぐみ




単項式と多項式 無料で使える中学学習プリント




高校数 数と式 整式 項 多項式 単項式とは オンライン無料塾 ターンナップ Youtube




中学数学と高校数学とのギャップ 単項式 多項式をめぐって 身勝手な主張




単項式 多項式と次数 ときどき係数 教遊者




文字式の重要な用語解説 単項式 多項式 項 同類項 定数項 係数 次数 数学fun




単項式の係数と次数 着目するポイントはこれだ 中学や高校の数学の計算問題




3分でわかる 多項式の解説 次数 昇べき 降べきの順をわかりやすく 合格サプリ




単項式の全てがこれでわかる 単項式の係数と次数 乗法 除法や多項式との違いまで 高校生向け受験応援メディア 受験のミカタ




体論 奇数次の項が現れない4次多項式 龍孫江の数学日誌




新単項式 多項式 項 係数 Youtube




単項式 多項式と次数 ときどき係数 教遊者




中2数学 多項式と単項式 10 11 赤城 ᐡᐤᐡ



0 件のコメント:
コメントを投稿