が,合同式を学習していない者にとっては理解が 難しい。また,合同式を用いた機械的な式変形で 記述されるため,証明の数学的な意味が分かりに くいという側面もある。そこで,本研究において は,合同式を用いずに,数学の予備知識があまり 合同式では、上のように $1^k$ や $(1)^k$ を作り出すように変形すると、余りがサクッと求められるようになります。合同式の便利な点はいくつもありますが、ここで見た内容はその一合同是矩阵之间的一个等价关系,经过非退化的线性替换,新二次型的矩阵与原二次型的矩阵是合同的。 数域P上n*n 矩阵 A,B称为合同的,如果有数域P上可逆的n*n矩阵C,使B=C'AC 矩阵 合同变换 是在矩阵左右两边分别乘C'和C,其中C为非退化矩阵

数a 合同式modとは Youtube
数学 合同式 入試
数学 合同式 入試- 1合同式 を で割った時の余りが等しい時、 は を法として、 と合同という。 と書く。 実際に を法として具体的に考える。 余りは3は3で割り切れる。 となる。 合同式の性質をまとめると下記のようになる。 例) の時 合同式 (congruence) a,b a, b は整数, c c は正の整数として, a− b a − b が c c で割り切れるとき a ≡ b (mod c) a ≡ b ( mod c) と書き, この形の式を 合同式 といいます また, このときの c c を 合同式 の 法といいます また, 上の式を以下のように書くこともあります a




合同式の問題の解き方 合同式の性質の証明 高校生向け受験応援メディア 受験のミカタ
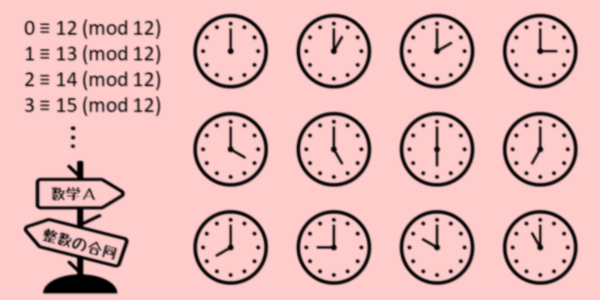
合同記号(ごうどうきごう)は、元来、合同式の合同(モジュロ)を表すための記号であり、「≡」(コングルエント)が使われる。 記号「≡」は、それ以外に、以下の意味 (幾何学的な)合同。 恒等式。;6講 合同式(1節 約数と倍数) 問題集3章 整数の性質です。わかりやすいポイントと例題つきの問題集です!定期テスト対策にお使いください。全て無料でダウンロードできます。塾や家庭教師、学校でご自由にお使いください!高校生のための現代数学講座 東京大学 「素数」 玉原国際セミナーハウス 講義(3) 坪井 俊 12年7月14日 「便利な合同式」 1 余りによる合同式と加法、乗法 • 定義 mを2以上の整数とする。「2つの整数a1 とa2 がmを法として合同である」こと
因みに、この合同式は、あのドイツの天才数学者ガウス(Johann Carl Friedrich Gauß;1777~1855)が提唱したもので、案外古い話である。 注記)数検準一級を受検する話ですが、状況によっては、今後、シリーズ化する可能性もあります。 このページでは、数学A「合同式」の問題と解答をまとめています。 合同式の計算、合同式と余り、合同式と証明など、合同式の問題一覧にしてあります。 目次1 合同式 問題と解答一覧2 合同式の解説 &n 合同式 (congruence) と書き, この形の式を 合同式 といいます また, このときの c c を合同式の 法といいます また, 上の式を以下のように書くこともあります プログラム経験のある人なら, a%c a % c という記号を使うと思いますが, 数学では mod mod を使います
演習問題 離散数学07p 合同式 合同関係 定義1 nを自然数とする。2つの整数x;y についてx y がnで割り切れるとき x y mod n と書き、xとy はnを法として合同であるという。この同値関係 による同値類を 合同類と呼ぶ。合同類の集合をZ=nZと書く。 例題1 1713 を3で割った余りを求めよ。(合同式の数学) 那須弘和(東海大学理学部情報数理学科) 1 今日は12年の7月22日で日曜日です 8日後の7月30日は何曜日でしょうか?答えは 簡単で8=71ですから, 日曜日の次の月曜日ですね では, 夏休みの終わる8月31日(40日 後)は何曜日でしょうか? 40 = 7£55 このページでは、数学Aの「合同式」について解説します。 合同式の公式、計算方法を,具体的に問題を解きながらわかりやすく解説していきます。 問題集を解く際の参考にしてください! 目次1 合同式(mod




合同式の原理の証明問題です F1 数学 箱根駅伝ブログ




高1 高校 数a 合同式 高校生 数学のノート Clear
だから, が成り立つ. ※初歩的な注意であるが,商 については,成り立たない. 合同式の四則計算 (2) のとき, を整数, を正の整数とすると (31) 両辺に同じ数を足してもよい (32) 両辺から同じ数を引いてもよい (33) 両辺に同じ数を掛けても整数の合同(ごうどう、英 congruence )は、数学において二つの整数の間に定められる関係である。 初めてこれを構造として研究したのはドイツの数学者ガウスで、1801年に発表された著書『Disquisitiones Arithmeticae』でも扱われている。 今日では整数の合同は、数論や一般代数学あるいは連立合同式・中国剰余定理の本質的な部分を理解するために,このページでは二元の場合で n 1, n 2 n_1, n_2 n 1 , n 2 が互いに素な場合のみを考えます。 より一般の場合は→中国剰余定理と法が互いに素でない場合への拡張
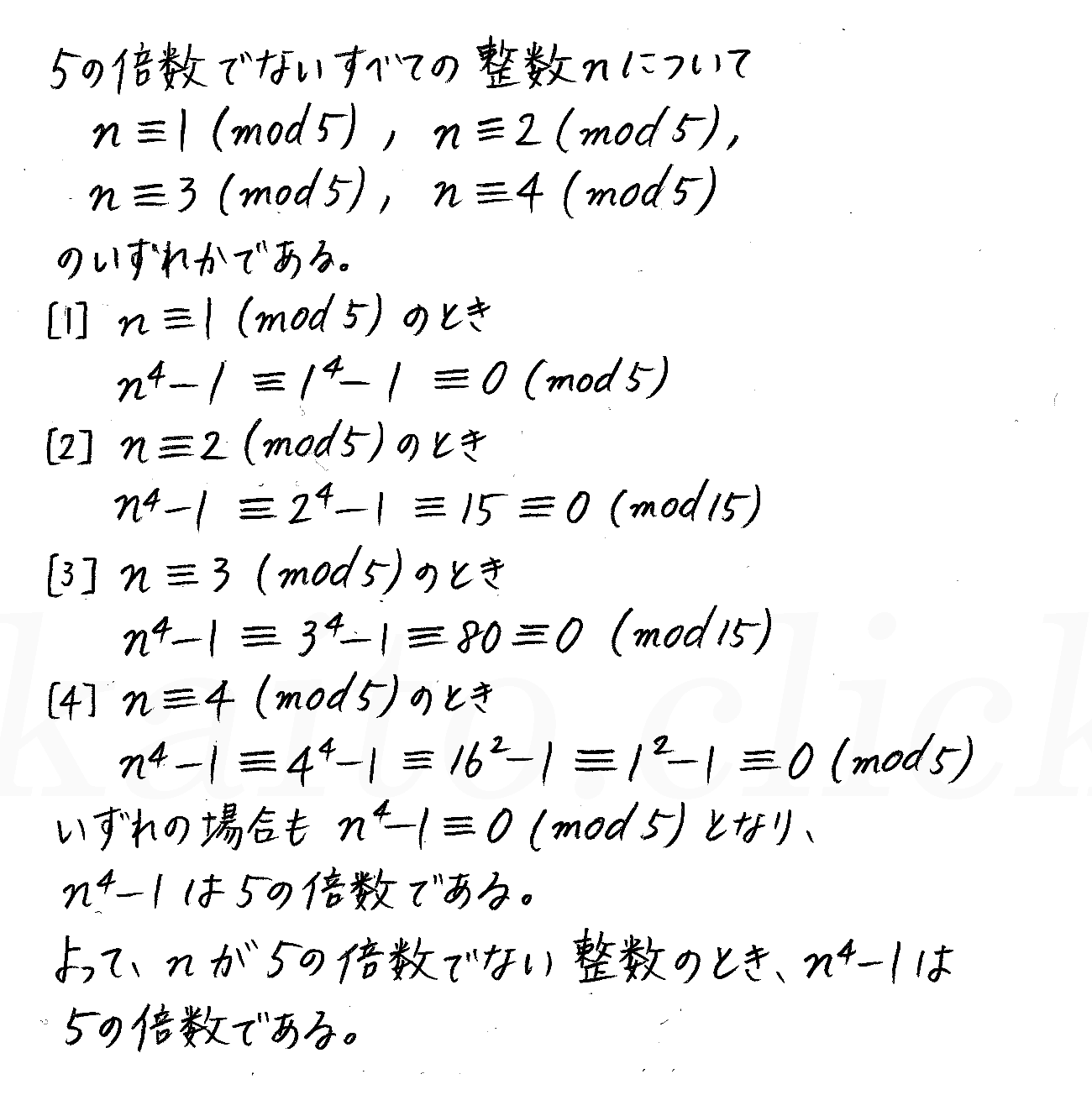



改訂版 4step数学a P161 発展 合同式




合同式 Mod の意味とよく使う6つの性質 高校数学の美しい物語
前回 https//googl/mNEhf1 次回 https//googl/VRrcbP動画のプリント(19ch) http//www19chtv/サブチャンネル とある男が 数学 高校生 約1年前 ともっち 合同式はabがmの倍数の時、a≡b (mod m)が成り立つという定義があります。 従って13≡1 (mod 144)も成り立つと思うのですがどうでしょうか?中1数学絶対値ってどういう意味? 中学生の勉強方法 123 中2数学連立方程式とは何だろう?その意味と解き方について解説します! 中学生の勉強方法 中2数学文字式の利用とは?「文字を使った説明」の仕方を解説!




合同式 Mod を応用して京大入試問題を解こう 不定方程式の問題も解説 遊ぶ数学
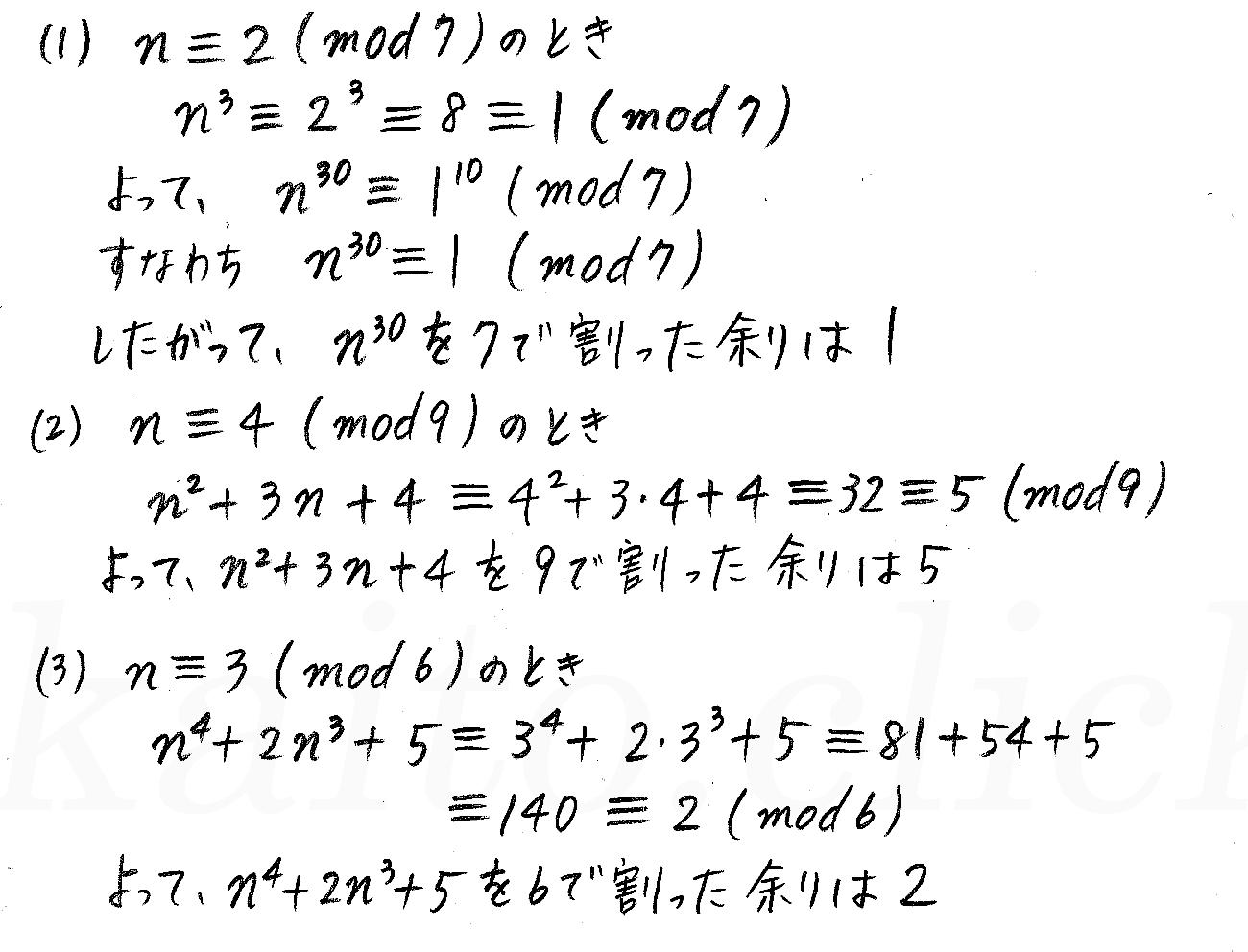



改訂版 クリアー数学a P162 発展 合同式
こんにちは。monologueの川村です。 今回は皆さんの多くが苦手意識を持っていたり、使用を避けている合同式の使い方、考え方について紹介します まずは合同式のおさらいから mを正の整数とする時、2つの整数a,bについて a−bがmの倍数であるとき、aとbはmを法として合同であるといい、a≡b (mod m合同式は、ざっくり言えば割り算の余りだけに注目して計算しましょう、という考え方です。 整数nを整数aで割った時の商をp、余りをqとすると、 n=apq と記述できます。これを合同式で表すと n≡q (mod a) となります(pが消えてしまいましたね) しかし、pが消えてしまっても、元が割り算で 合同式とはなにか 整数問題の中でも特によく出題されるのが剰余に関わる問題です.剰余とは余りのことで,たとえば,『$2^{40}$ を $7$ で割った余りを求めよ.』などのように余りを問う問題がよくあります.また,不定方程式の整数解を求める際にも,剰余の考え方を用いるこ



为什么有些初中生 觉得学数学无用 数学到社会上 真的没用吗 数学 初中生 中考




高校数学 発展 合同式 Modの利用 整数 Youtube
次の連立合同式の解のうち、もっとも小さい正の整数\(x\)を求めよ。 \\begin{align} x # 离散数学(数论基础) gonghr 博客园 离散数学(数论基础) 整除性 辗转相除 整除及其性质 定义511 :设a和b是任意整数,若存在整数c,使得a=bc,则称a是b的倍数,b是a的因数。 或者称a被b整除,而b整除a。 记为ba。 注意: (1)任意整数整除0 ,特别0




17考研数学 二 中如何判定矩阵合同关系 文都考研网



Ocw Nagoya U Jp Files 16 Eng C02 09 Pdf




合同式 数学aの教科書から自由に考える 身勝手な主張




特別な合同式を解いてみよう 身勝手な主張




合同式 Mod の成り立ち Well Definedの意味を考える 数学の部屋




数の構成 合同式で遊ぼう 掛けてもいいなら割ってもいい 大人が学び直す数学



4 剰余類 合同式を使う問題 京極一樹の数学塾




1研究中 C 数学11 図形の証明 合同 相似 合同式 Mod余りの数 チェバの定理メネラウスの定理




整数問題へのアプローチ 10 合同式の定義と性質とその証明 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学の整数の性質で合同式の学び直し 第3回は加法と合同関係 大学受験対策にも タロウ岩井の数学と英語 Note




合同式 数学aの教科書から自由に考える 身勝手な主張




整数問題へのアプローチ 15 合同式でよくある誤用 考察 怜悧玲瓏 高校数学を天空から俯瞰する




受験数学 2 合同式 Youtube




数学 Modってなによ 実は便利な合同式を解説 合同方程式も 大学生の勉強部屋




香川大学工学部 富永浩之 情報数学1 第2 2章 合同式の逆元と応用 香川大学工学部 富永浩之 Ppt Download




1研究中 C 数学11 図形の証明 合同 相似 合同式 Mod余りの数 チェバの定理メネラウスの定理




合同式の問題の解き方 合同式の性質の証明 高校生向け受験応援メディア 受験のミカタ




合同式 書き方に注意 数学の偏差値を上げて合格を目指す




もっとmod 合同式の使い手になれる動画まとめ Okenavi




数学草稿 知乎




Kamimura 整数1次合同式1次不定方程式 整数解 特殊解 一般解 数学のブログ T Co Uzfhbxjnsp 数学 代数学




の ア で X 2 4 Mod6 2 4 Mod6 の式が分かりません Clear



48s96ub7b0z5f Net Goudoushiki Houteishiki




合同式 数学aの教科書から自由に考える 身勝手な主張




武田塾 宮崎校 15 九州大学 理系数学のお手軽解答 赤本の解答では二項定理や帰納法 背理法を用いた解答でしたが合同式と互除法を利用した別解です 学校ではあまり触れない合同式やgcdの記述法を知る事でシンプルに解けるようになります 整数問題




关于大学数学概念学习的一些实例分析 参考网



高校数学合同式 1 で最後に9 2 Mod7 とありますが2が出てく Yahoo 知恵袋




Download Mp4 Mp3 3gp Naijagreenmovies Fzmovies Netnaija




S Live数学館 V Twitter 数研スタンダード数a 3章 整数の性質 29合同式 問題254 255 256 P143 合同式 A B Mod M の仕組みを理解 すると 割り算の余り 商 への理解 が早まります 例題に取り組めば容易に理解できる はずです 食わず嫌いにならないように




合同式の問題の解き方 合同式の性質の証明 高校生向け受験応援メディア 受験のミカタ




山と数学 そして英語 高校数a 合同式とは何か



水木艾迪考研数学解题36计之28 等价相似与合同下载 在线阅读 爱问共享资料



数学ナビゲーター掲示板 One Thread Res View 合同式の計算 Page 0




ユークリッドの互除法は無理という人へ 不定方程式は合同式を試してみて 数学のコツ壺 風いま数学協室




高校数学 数a 勉強動画 合同式の問題 19ch




高校数学の整数の性質について合同式の計算で大きな指数の余りを求める タロウ岩井の数学と英語 Note



高校数学の合同式について 4 31を27で割った余りを求めよとい Yahoo 知恵袋



4 剰余類 合同式を使う問題 京極一樹の数学塾




差がつく 合同式 基本編 数学の2次試験で合同式を使いこなす マスマス学ぶ




风靡全球的印度式数学窍门 东东购 Easterneast



Fdkyb3b9c093sr81e Com E6 95 B4 E6 95 B0 E5 95 8f E9 A1 8c E9 80 A3 E7 Ab 8b E5 90 E5 90 8c E5 8f
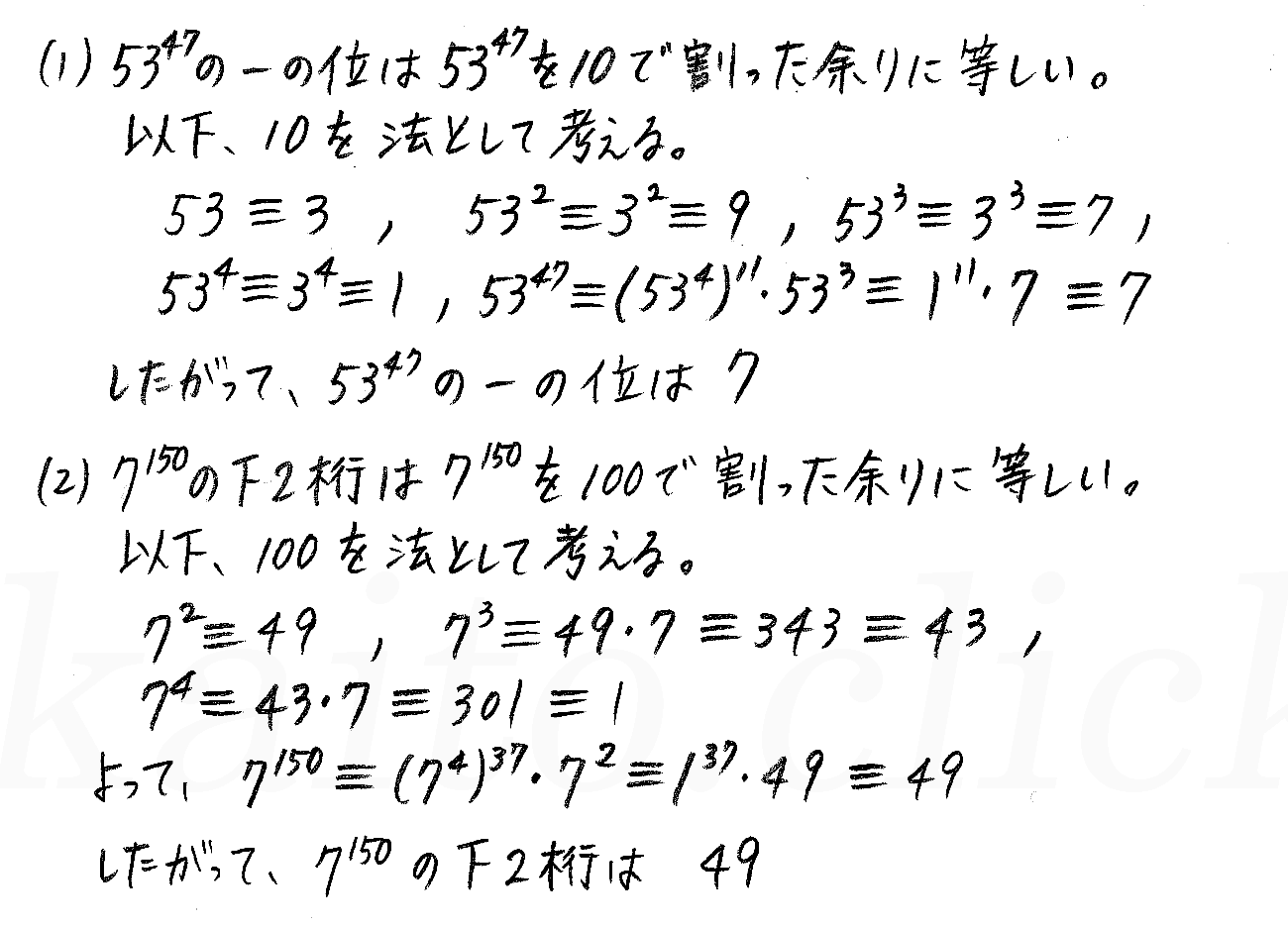



改訂版 クリアー数学a P162 発展 合同式




問題 4 2n 1 3 N 1 は13の倍数であることを示す 数学好きの大学受験数学




数学 英語のトリセツ おすすめch紹介 ページ 8 意味とは何




整数問題へのアプローチ 14 合同式でよくある誤用 解答例 怜悧玲瓏 高校数学を天空から俯瞰する




房屋租赁合同范本图片 正版模板下载 摄图网




改訂版 4プロセス数学a P180 補 合同式で表される方程式




高校数学の整数の性質の学び直しで合同式の定義を書き換える 大学受験対策にも タロウ岩井の数学と英語 Note




Gold Standard 数学特講 多項式の合同式 ガチノビ



数学i Aチェック リピート 第6章 3整数の性質 4 合同式 Pukiwiki




合同式




合同式 身勝手な主張




一道德国数学竞赛题 仅有1 的学生能在5分钟内解出 思路很难 一次方程 因式分解 构造 网易订阅




合同式 Mod の問題と使い方を超わかりやすく説明してみた 理系ラボ




香川大学工学部 富永浩之 情報数学1 第2 1章 合同式の性質と計算 香川大学工学部 富永浩之 Ppt Download




合同式 おいしい数学



高校数学合同式を使って証明するのですが 僕の書き方でも問題ないですか Yahoo 知恵袋



受験 テスト向けに中学 高校で知っておくといい大学数学 倍数判定 合同式 Mod 編 Citrussinのチラシの裏




大学受験 高校受験 数学 整数 合同式 mod 5 7 Mod 3 さくらの個別指導 さくら教育研究所 Skredu
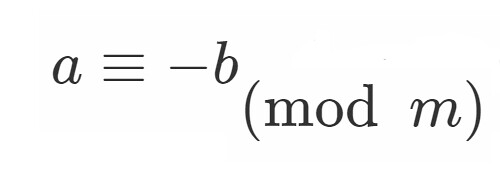



合同式でなぜマイナスが使えるのか もう一人のy君



タロウ岩井の数学と英語 Noteの補足など 高校数学の合同式の性質を学び直し 大学受験対策にも Powered By Line




合同式 Mod を応用して京大入試問題を解こう 不定方程式の問題も解説 遊ぶ数学



数学 合同式の問題です 2 N 1が7の倍数となるのは自然 Yahoo 知恵袋




余りを求める合同式の計算が分からないので 詳しく教えていただきたいです Clear




数の構成 合同式 は割り算と余りの式 大人が学び直す数学
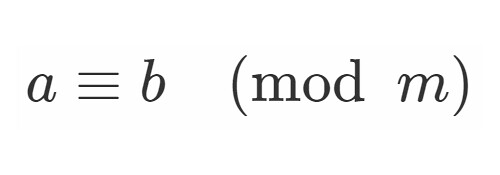



数学 合同式の基本性質 もう一人のy君



48s96ub7b0z5f Net Amari Goudoushiki




数学a 合同式を使って入試問題を解いてみよう 日々是鍛錬 ひびこれたんれん




Images Of Disquisitiones Arithmeticae Page 4 Japaneseclass Jp




2016年 東大文系数学 第4問 小学生でも解ける 整数 合同式 東大に文理両方で合格した男が綴る 受験の戦略




数a 合同式modとは Youtube




整数問題へのアプローチ 14 合同式でよくある誤用 解答例 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学a 合同式の定義と性質 A B Mod M 受験の月




受験で使える合同式その4 5分で解ける 整数問題の証明 大学入試 Youtube




合同式の考え方が分かりません 教科書に書いてあることは気にしないでください Clear



数学a 整数の問題で合同式を使ってみよう 日々是鍛錬 ひびこれたんれん




整数問題へのアプローチ 13 合同式でよくある誤用 問題例 怜悧玲瓏 高校数学を天空から俯瞰する




数学 使えると便利 合同式をマスターしよう Monologue Note




初二数学上册第十四章节因式分解易错点 题型整理 三好网




合同式 Mod の意味とよく使う6つの性質 高校数学の美しい物語




香川大学工学部 富永浩之 情報数学1 第2 2章 合同式の逆元と応用 香川大学工学部 富永浩之 Ppt Download




山と数学 そして英語 高校数a 合同式の利用 その2




数学オリンピック 合同式の割り算




工程承包合同数学下载 Word模板 爱问共享资料



上海交通大学 难考了 数学考研李扬 微信公众号文章阅读 Wemp




跟锦数学1806




高校数学 発展 合同式 Modの利用 整数 Litetube




合同式 定義 性質 使い方 をマスターしよう 高校数学a 整数 数学の部屋 Youtube




集合と合同式による確率の解法 数学 津曲塾




合同式のプリントを作りました 算数 数学専門塾 算数の極意



タロウ岩井の数学と英語 Noteの補足など 高校数学の整数の性質で合同式の推移律 大学受験対策にも Powered By Line




改訂版 クリアー数学a P166 発展 合同式で表される方程式



0 件のコメント:
コメントを投稿