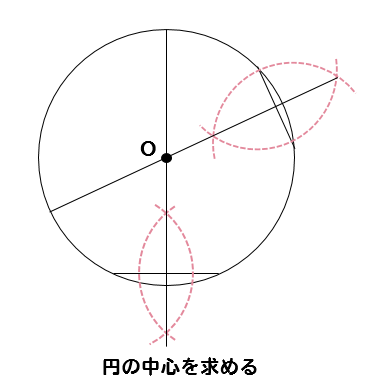
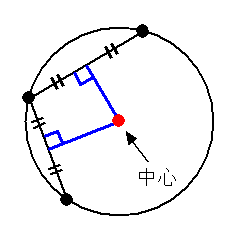
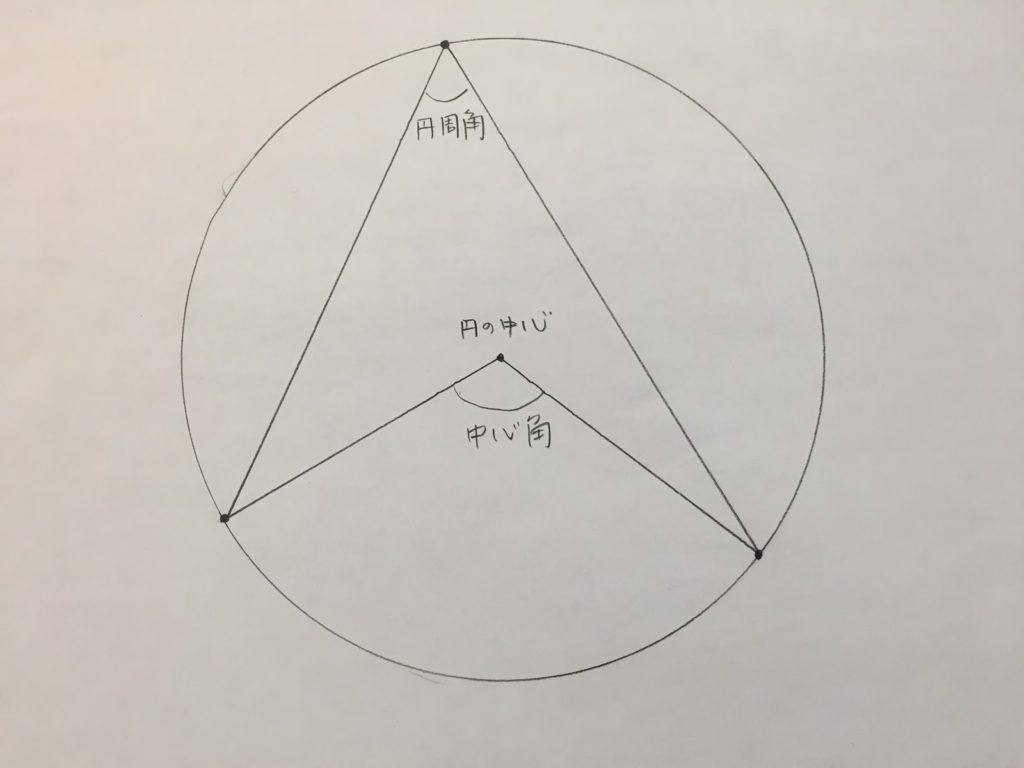
④No12以降の各中心杭までの弧長は、中心杭間距離000mを逐次加えて求め、それに対する偏 角は、中心点杭間距離に対する偏角δを、加えることにより求める。 例えば、No12の杭は、 ° ¢ ² ° ´ ´ = 5 43 57 314 180 2 m 000m δ= であるから、IPから円の中心の求め方 三角定規でなくても良いのですが、直角部分を円の任意の箇所に置きます。 底辺と円の交差する点をa、もう一方の高さ部分と円の交差する点をbとし、aとbを直線で結びます。 その線にやや直角位になる様に三角定規を移動し、同じ方法では,円の方程式の導き方を確認しましょう。 ここでは,『「円周上の点」と「中心」の距離』と『半径』が同じということを利用して,円の方程式を導いてみます。 さらに,この式を展開して整理すると, x 2 y 22ax2bya 2 b 2r 2 =0 となります。
Studydoctor円の公式と なぜ 中学1年数学 Studydoctor
円の中心の求め方 cad
円の中心の求め方 cad- 弧長(円弧の長さ)L、弦長d、矢高(円弧の高さ)h、半径rのどれか2つに値を入力して、残りの2つを0と入力すると(空白にはしないでください)、その残りの2つおよび中心角を計算します。 L=r*θ, d=2*r*sin (θ/2), h=r* (1cos (θ/2))を用い、ニュートン・ラフソン円の中心、半径を求める練習問題! まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! こちらの関連記事はいかがでしょうか?




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
円の中心の求め方 数学 ケガキについて 工学 4 ミリのステンレスに穴を開けたい diy・エクステリア 5 作図により円の中心の求める方法について質問です。 ①ある円で任意の異なる4点a,b,c,dをとる。 扇形の中心角の求め方3パターン を見てみてね ちなみに、 中心角を求める公式 もあって 中心角 = 360× 半径 母線 中 心 角 = 360 × 半 径 母 線 こんなのもあるから、今日テストの人はさっと覚えてもいいかもしれないね けど! 何を求めるのも公式だより傾きm を求めて,接線を作る 2円の位置関係 ①2円の中心、半径を求める ②2円の中心間の距離を求める ③②の中心間の距離と半径の和・差を比較する 2円の交点を通る円・直線 2円x y lx my n2 2 0 、x y px qy r2 2 0 の交点を通る
4、aとbを結んだ線の真ん中の点が、この円の中心になります。(oの点) 5、紙を空き缶に乗せて、求めた円の中心をクギなどで印を付ければできあがり! これは、円周角の定理を使った円の中心の求め方です。 円周角の定理とは 円周角の定理とは、Vy = (float)MathSin (rad) * r oy; こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の外心(垂心)」 について、性質の証明や座標の求め方、位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心とは なぜ"外心"なのか、いきなり説明することは困難です。
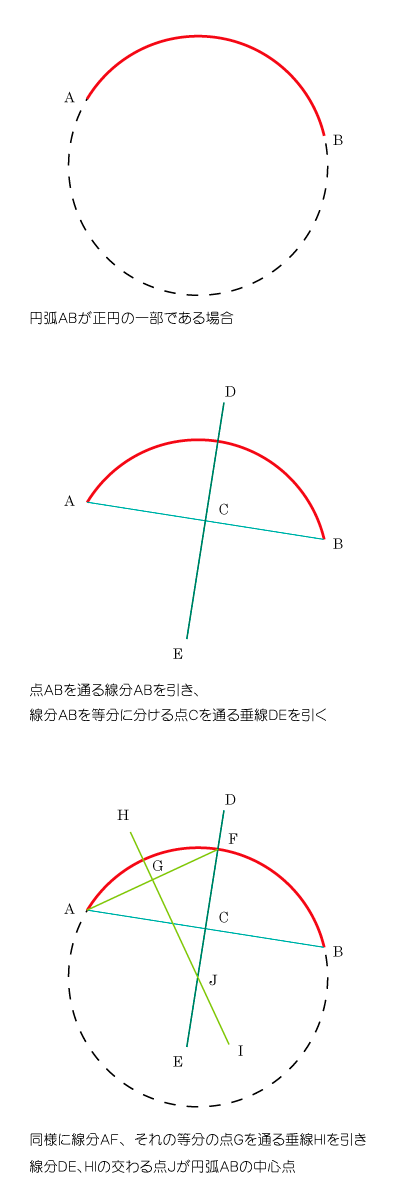
三角形abc の内接円,外接円の中心(半径)をそれぞれi(r),o(r)とし, io= d とすると, rd rd r 1 (証明1)i を通り,oi に垂直な弦をpq とすると, opi は ∠pio=90°の直角三角形であるから, 三平方の定理より pi 2 r2 d2 ① 方べきの定理より ai id iqpi 2 ② ①,②求めたい円弧の半径を X とします。円弧の幅を W とし、高さを H とします。求める X はピタゴラスの定理から上の式のようになります。これを展開したものが下の式です。 この X を半径 R として、円弧の両端から円を描き、その交点 C が円弧の中心です。 円とは, 平面上において,ある点からの距離が等しい点の集合でできる曲線 のことです。 「ある点」を 中心 ,中心から円周上の点までの距離を 半径 と呼びます。




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
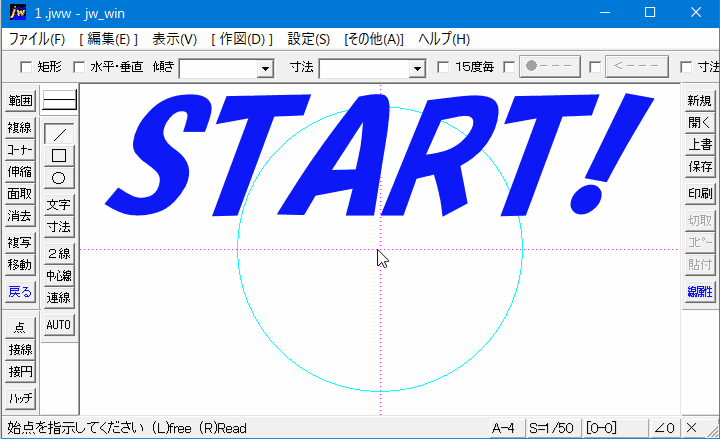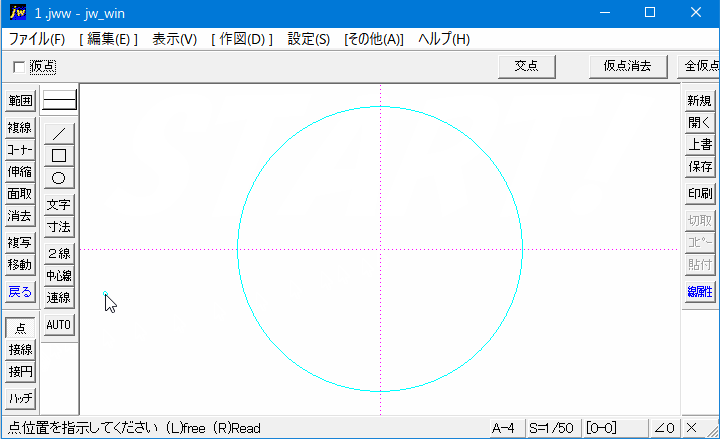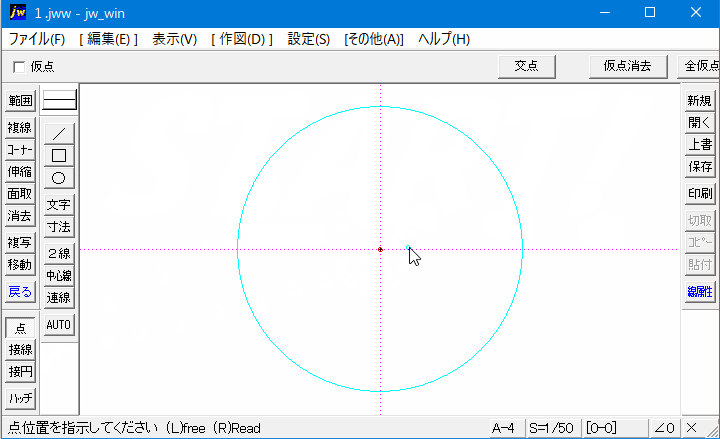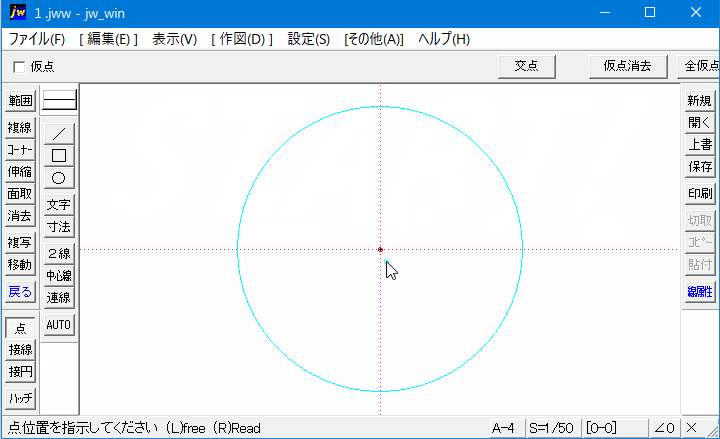
3点を通る円POINT 円の通る3点から中心・半径を求める一般式を導出する. 導出した式で計算フォームを作成. Excelにコピペして使えるフォーマットあり. 単純な「連立方程式」の問題ですが,一般解は少し複雑な形になります. 計算フォーム Excel用フォーマット 導出 円の方程式 円の中心 円そこで今回は、すでに描いた円の中心点を簡単にだす方法をご紹介させていただきます。 円の中心点を簡単に出す方法 今回使用するJw_cadの便利な機能は『 クロックメニュー 』という機能です。 まずは、キャプチャー動画で操作手順をご確認ください。円周を8等分した点です x, y, z の角度を求めましょう →1コマあたりの中心角は 360°÷8 = 45° xは3コマ分の中心角の半分 (=円周角) → x = 1 2 1 2 (3×45°) = 135° 2 135 ° 2 = 675° 同様に、yは2コマ分の中心角の半分 → y = 1 2 1 2 (2×45°) = 90° 2 90 ° 2 = 45° 同じ弧より



作図 円に内接する正三角形の作図方法とは 数スタ



3点を通る円 と 2点とある直線上に中心がある円 の方程式の求め方
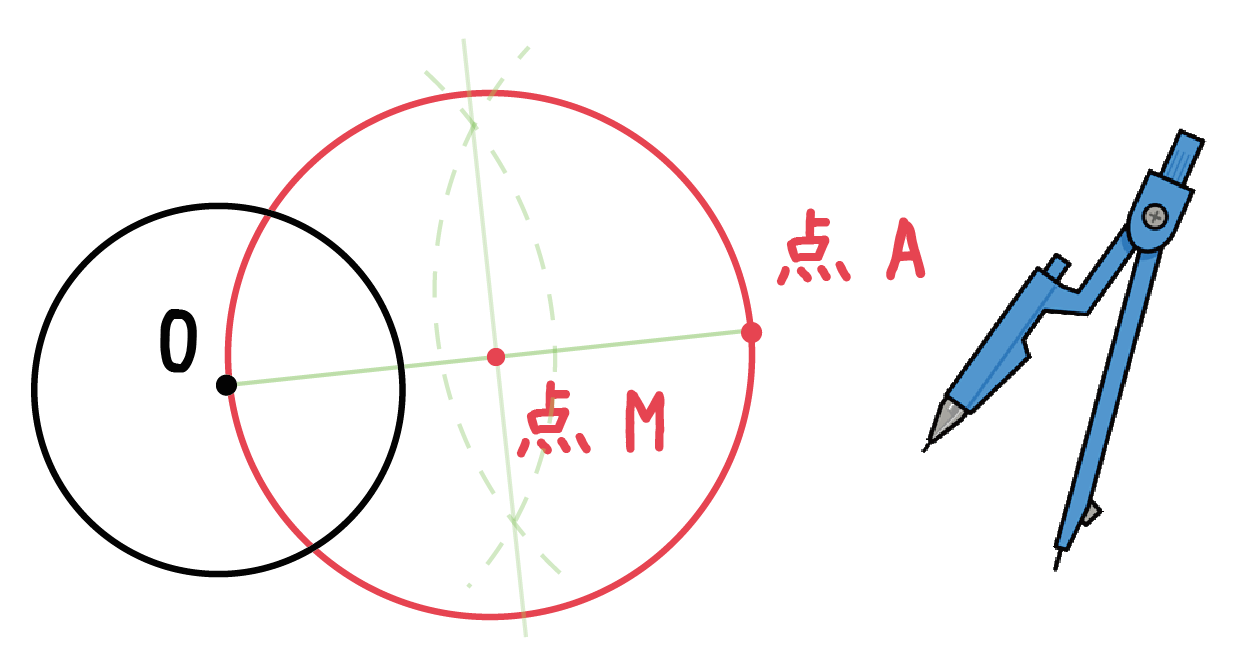
このように 「原点が中心の円」 で 「接点が ( x 1 − a, y 1 − b) である接線の方程式」 を考えることになります。 ここがミソです。 そうすると先ほど私たちが覚えた接線の公式が使えて ( x 1 − a) x ( y 1 − b) y = r 2 とできますね。 あとは 円を元の位置 曲尺(図1)という直角に曲がった定規を用いれば、円の直径や中心を求められ、丸太から無駄なく木材を切り出すことができる。 円周上の任意の点Aに曲尺の直角部分をあて、A以外の曲尺と円との交点をB,Cとし、点Bと点Cを結ぶ( "曲尺を使い円の中心を求める 1(準2級)" の続き次に、中心角について解説していきます。 中心角を一言で言うと、円周角の中心バージョンです。 円周角では、点を円周上に3つ置きましたが、円周上に2つ置いた点と、円の中心をそれぞれ結んだときに出来た角を中心角といいます。 これを図にすると、




標準 3点を通る円の作図 なかけんの数学ノート



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典
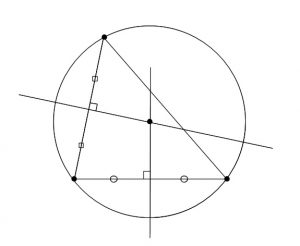
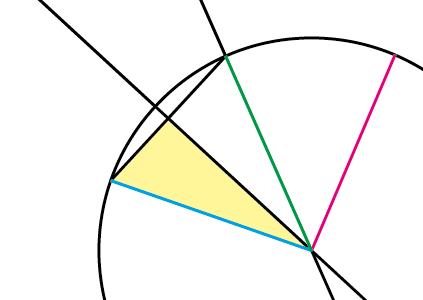
更新 1254 編集 jdash00 概要 円弧の一部から円の中心を見つけることができるのはなぜなのかを作図ソフトのIllustratorを使って考えてみました。 「 正確に円弧をトレースするためのTips DTP Transit 」を読んでいて、正直何をしているのか意味がすなわち,上記の偏心(a,b)を決定し,それを中心と した同心円でワーク形状を挟んだ場合の半径差が真円度と なることを意味している. 5.真円度と基準円 真円度の求め方には,基準円を元に以下の4つの方法が ある3). 1.最小領域真円度/最小領域基準円進研ゼミからの回答 円周上の点はどこでも,円の中心から等距離であるという性質を利用します。 円周上に適当な3つの点を決め,その3点から等距離にある点を作図から求めます。 ここで紹介している内容は17年3月時点の情報です。 ご紹介している




円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
3点を通る円の中心と半径を求める 点 A (x 1, y 1) 、点 B (x 2, y 2) 、点 C (x 3, y 3) を通る円の中心 P と半径 r を求める。 三点を通る円の中心座標と半径を求める公式を教えてください。ちなみに3点はa(-4,3) b(5,8) c(2,7) です。高校の頃にやった覚えがあるのですが、現在大学4年になりまして、すっかり忘れてしまいました。どなたか知っている方がいら右図5において,原点を中心とする半径5の円の方程式を求めてみよう. 円周上の点 P の座標を (x , y) とおくと,ピタゴラスの定理(三平方の定理)により, x 2 y 2 =5 2 (A) が成り立つ. 上半円については, y ≧ 0 なので, y= (B)




円の中心の座標と半径を求める問題です 答えと解説を画像付きで送ってください Clear




三角定規で円の中心を作図 おときち副塾長 電脳空間学習塾かもん Youtube
3つの点から円の方程式を求める 円の方程式は の他に ① と表すこともできます。 ※円の中心、半径の長さがわかる時に使用 ※3つの点を通ることがわかっている時に使用 このようにして使い分けます。 それでは早速、①を使っ例題 上節でみたように,$2$ 円の位置関係を調べるには,$2$ つの円の半径と,中心間の距離を調べればよいのでした.円の方程式からその中心の座標と半径を求める方法は前記事 →円の方程式の表し方 で紹介しています.これらの知識を用いて,実際にいくつかの例題を解いてみましょう. 円の方程式とは? 円の方程式とは、 中心の座標と円の半径を用いて、円を方程式で表したもの です。 表し方には「基本形」と「一般形」の \(2\) 通りがあります。 基本形の公式 円の方程式を基本形で表現すると、円の中心と半径が一目でわかります。



数学 円弧から円の中心が割り出せるのかを検証してみた 円弧のトレース用




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
中心Oの求め方 ではまず、点A、点Bから等しい距離にある点を求めてみましょう。 先ほど示した垂直2等分線を使います。 ABを垂直に2等分する線abは、上の図のようになります。 つまり、 垂直2等分線の性質から、線ab上にある点は必ず点Aと点Bから同じ 動画による解答は以下になります 数学円の接線の方程式の求め方(解法③:接点を求めて計算量を軽くしたい)高校 数学 図形と方程式 数学2(質問ありがとうございます! ) (下の解説を読んだ後の方がわかりやすいかと思います) では実際中心(a,b)で半径r、円周の任意の点を(x i,y i)とすると円は以下の式で表せます。 rと中心とx i,y i 間の距離の差を出す式をとりあえず差を0として作成します。 上記の式を二乗すると 左式を使って上式からカッコを取り除きシンプルにします。




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




車の 最小回転半径 Park Blog
Re円の座標の求め方 投稿記事 by 2³ » 1 year ago 僕はC#使ってるのでC#での説明になってしまいますが、 vx = (float)MathCos (rad) * r ox;




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円の方程式の求め方まとめ パターン別に解説するよ 数スタ




円の中心の作図 コンパスを使って求める方法とは 中学数学 理科の学習まとめサイト



Jw Cad 円の中心点の出し方




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




円の中心を求める 3つの方法 Wikihow




円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト




円運動の公式まとめ 運動方程式 加速度 遠心力 向心力 理系ラボ




垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア




差し金テク 円の中心と直径を限りなく正確に求める方法 男のレシピ帳




最後の2円の中心間の距離の求め方が分かりません Clear




円の中心を求める 3つの方法 Wikihow
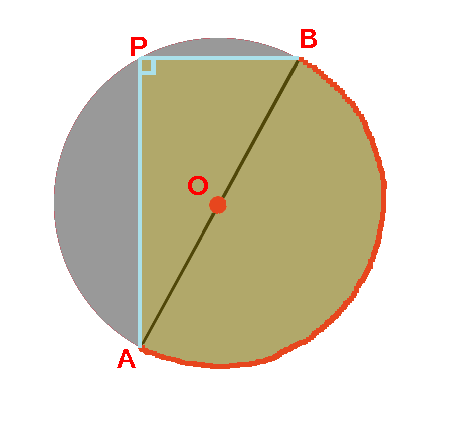



空き缶の中心の見つけ方 綿菓子を自宅で作ろう




円の中心を求める 3つの方法 Wikihow



From灘 円の中心の求め方 朝日小学生新聞 中学受験eye 関西圏




基本 円の方程式 なかけんの数学ノート
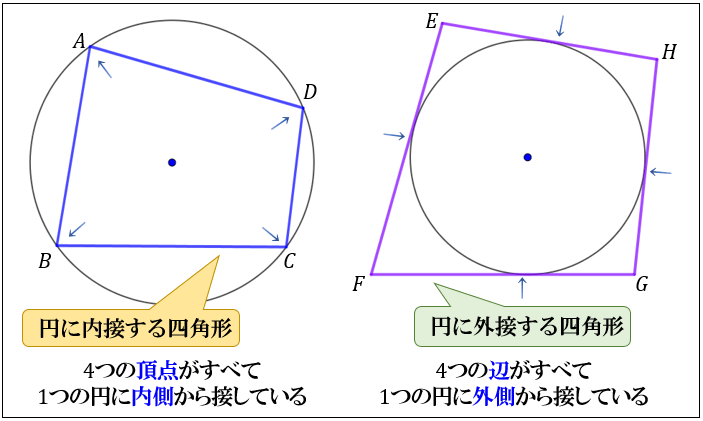



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




円の中心を求める 3つの方法 Wikihow




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




作図 05 円の中心の求め方 Youtube



Studydoctor円の公式と なぜ 中学1年数学 Studydoctor



円の中心の求め方 Love金沢水彩画



幾何計算 2点と半径から円の中心点を求めます Satoh



こんにちは 円の中心を通らない場合どうやって解いたらよいかわかりま Yahoo 知恵袋
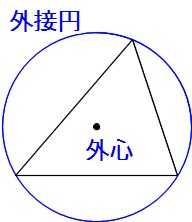



Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ



円の中心を求める方法を教えてください 条件 小学生にも理解 Yahoo 知恵袋



1




差し金テク 円の中心と直径を限りなく正確に求める方法 男のレシピ帳
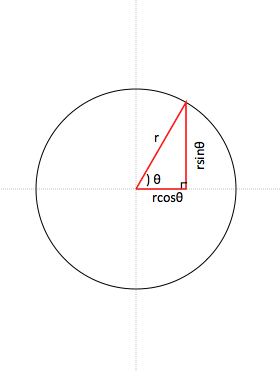



円の中心からの角度から真円の円周上の座標を計算する Gamesprit
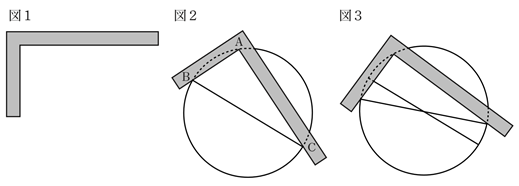



曲尺を使い円の中心を求める 1 準2級 カワズの数学ノート 数学検定 準2級




垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




円周の求め方 公式は直径を使うので 半径と間違えないように 中学や高校の数学の計算問題



外接円とは 半径の公式や求め方 性質 書き方 受験辞典



1




円の中心の出し方 コンパスなし 直径わからない編 シャンハイ山本弾工房



3次元空間での円の中心の求め方 Inak Engineering Llc



円周角




おうぎ形の中心角の求め方 Youtube
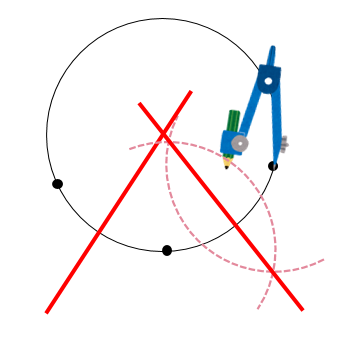



中1 作図 円の中心を求める方法を解説 数スタ




中心角の求め方が即わかる 合わせて知りたい知識とは 高校生向け受験応援メディア 受験のミカタ
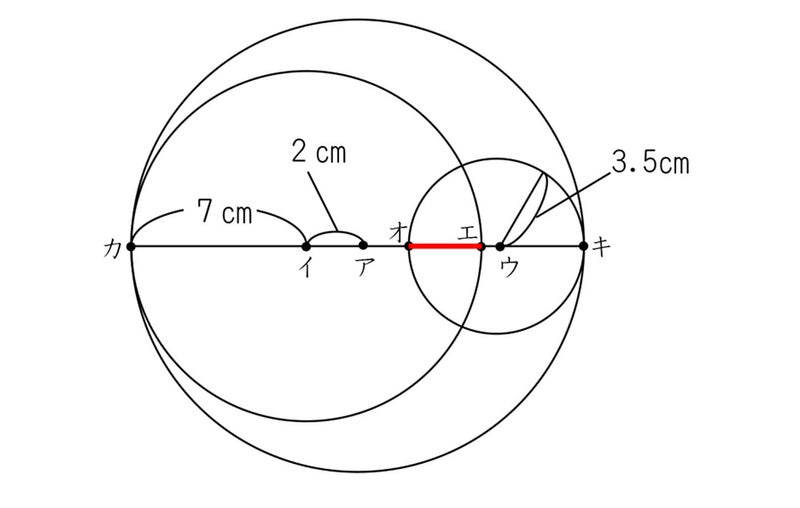



小学三年生と円の問題を考えてみる そらいろ日記 言葉の宝箱




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円の方程式 数学ii フリー教材開発コミュニティ Ftext
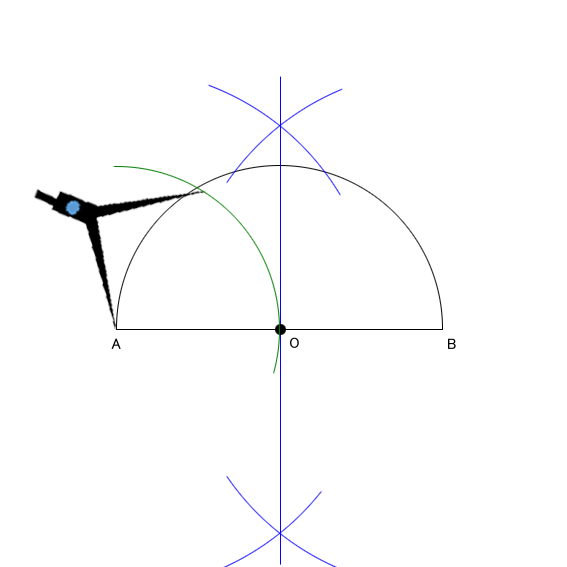



平面図形 おうぎ形 4 ネット塾




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




扇形の面積の求め方 公式と計算例




Aの求め方を教えてください 点oは円の中心です 答えは174 です Clear




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト




円の中心を求める 3つの方法 Wikihow



数学 円弧から円の中心が割り出せるのかを検証してみた 円弧のトレース用




2つの点から円の方程式を求める 数学ii By Okボーイ マナペディア




3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ



内接円とは 内接円の半径の公式や求め方 性質 書き方 受験辞典




差し金テク 円の中心と直径を限りなく正確に求める方法 男のレシピ帳




垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア



差し金テク 円の中心と直径を限りなく正確に求める方法 男のレシピ帳




円の中心を求める 3つの方法 Wikihow




円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく




中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円の中心を求める 3つの方法 Wikihow



1



算数 数学 働きアリ The 2nd




1数 作図による円の中心の求め方 Youtube



おうぎ形の中心角の求め方 Youtube



中心角は円周角の2倍になる




四角形の中心の求め方 四角形の中心 真中 の求め方は 各辺の真中を添付 Okwave



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典



円に接する直線 接線の方程式 の求め方3パターン




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




Processing 2点を通る直線と円の交点を求めよう Zawaworks S Diary
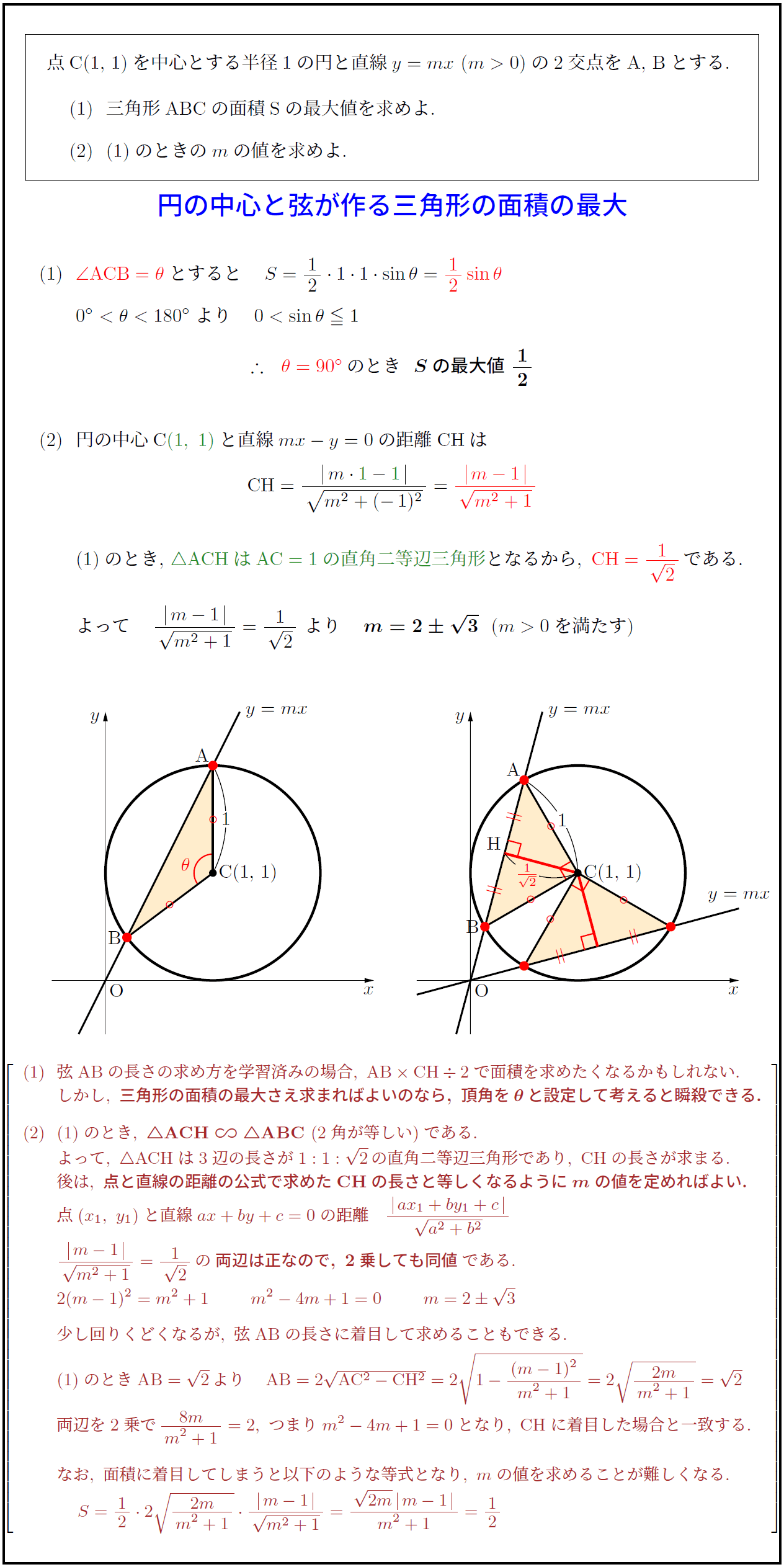



高校数学 円の中心と弦が作る三角形の面積の最大 受験の月



空き缶の中心の見つけ方 綿菓子を自宅で作ろう




円の中心を求める 3つの方法 Wikihow




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




Aの求め方を教えてください 点oは円の中心です 答えは174 です Clear
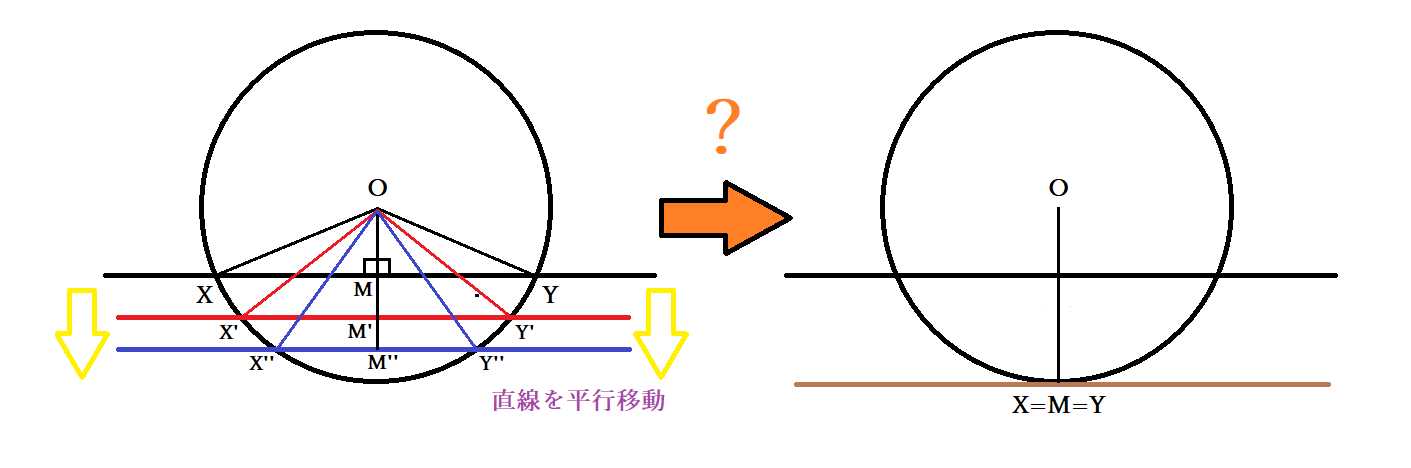



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog




数学 円弧から円の中心が割り出せるのかを検証してみた 円弧のトレース用
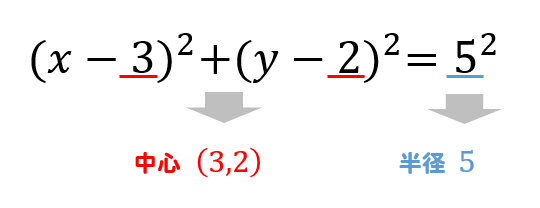



円の方程式 中心の座標と半径の求め方を解説 数スタ




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
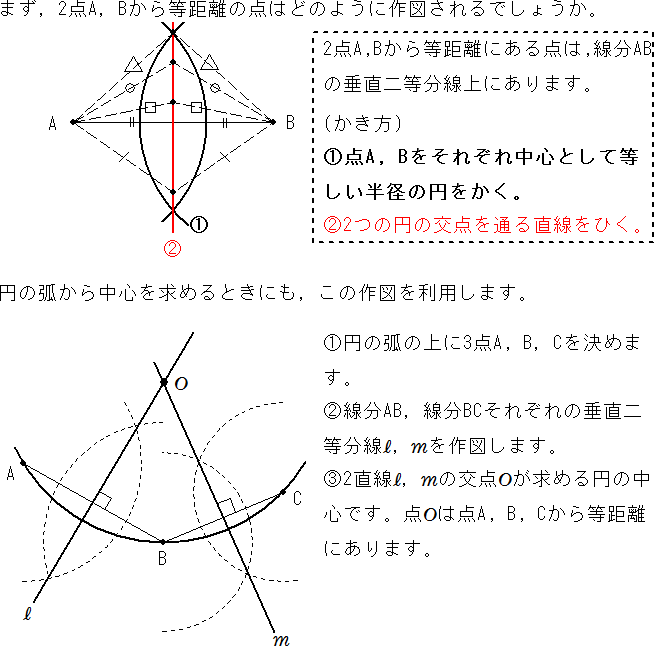



平面図形 円の中心を求める作図 中学数学 定期テスト対策サイト




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



点oは円の中心です Xの求め方がわかりません 解き方を教えてください Yahoo 知恵袋



0 件のコメント:
コメントを投稿